This is an old revision of the document!
Dipole antenna radiation pattern derivation
For a dipole antenna centered on the origin and oriented along the z axis with length L, the far-field radiation pattern can be derived as follows:
The current on the antenna will be approximately sinusoidal, with zeros at the ends of the antenna, represented by
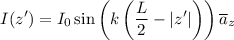
where
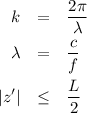
Use the current distribution to find the Z component of the vector potential
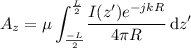
where
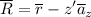
and the magnitude of R can be approximated as
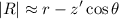
Substituting yields
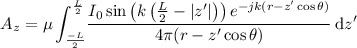
As 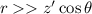 ,
, 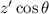 can be neglected in the denominator. However, it cannot be neglected in the exponential as it is a phase offset.
can be neglected in the denominator. However, it cannot be neglected in the exponential as it is a phase offset.
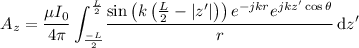
rearranging yields
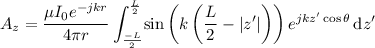
Eliminate the absolute value by splitting into two integrals:
![Equations \begin{eqnarray*}
A_z = \frac{\mu I_0 e^{-jkr}}{4\pi r} \left [ \int_{\frac{-L}{2}}^0 \! \sin \left( k \left( \frac{L}{2} + z' \right) \right) e^{jkz' \cos \theta} \, \mathrm{d}z' \right. + \\
\left. \int_0^{\frac{L}{2}} \! \sin \left( k \left( \frac{L}{2} - z' \right) \right) e^{jkz' \cos \theta} \, \mathrm{d}z' \right ]
\end{eqnarray*}](/wiki/lib/exe/fetch.php?media=wiki:latex:/img7170c42470c4aff05484816350603663.png)
Flip limits on the first integral and combine
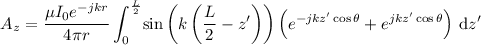
Substitute 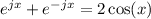
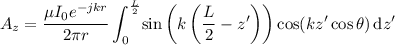
Now, integrate it, setting aside the constants and limits temporarily:
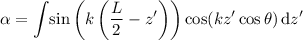
Integrate by parts (tan cow):
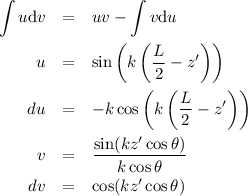
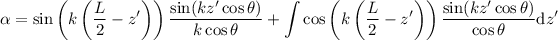
And again:
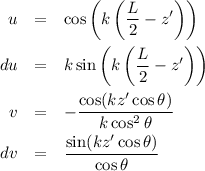
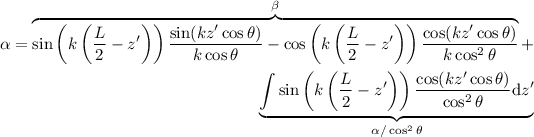
Time for some algebra:
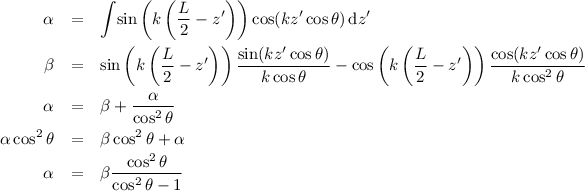
so
![Equations \begin{eqnarray*}
\alpha = \left [ \sin \left( k \left( \frac{L}{2} - z' \right) \right) \frac{\sin(kz' \cos \theta)}{k \cos \theta} - \cos \left( k \left( \frac{L}{2} - z' \right) \right) \frac{\cos(kz' \cos \theta)}{k \cos^2 \theta} \right ] \frac{\cos^2 \theta}{\cos^2 \theta -1}
\end{eqnarray*}](/wiki/lib/exe/fetch.php?media=wiki:latex:/img0bb980ae71d4a39d3b800577f329960b.png)
Now substitute 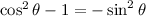
![Equations \begin{eqnarray*}
\alpha = \frac{1}{k \sin^2 \theta} \left [ \cos \left( k \left( \frac{L}{2} - z' \right) \right) \cos(kz' \cos \theta) - \sin \left( k \left( \frac{L}{2} - z' \right) \right) \sin(kz' \cos \theta) \cos \theta \right ]
\end{eqnarray*}](/wiki/lib/exe/fetch.php?media=wiki:latex:/img1cf6e9d3f9b3c5eba73d2a495f6b6b73.png)
and plug in the limits 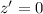 and
and 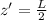 and bring back the constants
and bring back the constants
![Equations \begin{eqnarray*}
A_z = \frac{\mu I_0 e^{-jkr}}{2\pi r k \sin^2 \theta} \left [ \cos \left( k \left( \frac{L}{2} - \frac{L}{2} \right) \right) \cos(k\frac{L}{2} \cos \theta) -\\
\sin \left( k \left( \frac{L}{2} - \frac{L}{2} \right) \right) \sin(k\frac{L}{2} \cos \theta) \cos \theta - \\
\cos \left( k \left( \frac{L}{2} - 0 \right) \right) \cos(k 0 \cos \theta) +\\
\sin \left( k \left( \frac{L}{2} - 0 \right) \right) \sin(k 0 \cos \theta) \cos \theta \right ]
\end{eqnarray*}](/wiki/lib/exe/fetch.php?media=wiki:latex:/img52084f70f59c3027e4e9ecedd6a0e189.png)
simplify
![Equations \begin{eqnarray*}
A_z = \frac{\mu I_0 e^{-jkr}}{2\pi r k \sin^2 \theta} \left [ \cos \left ( \frac{kL}{2} \cos \theta \right ) - \cos \left( \frac{kL}{2} \right) \right ]
\end{eqnarray*}](/wiki/lib/exe/fetch.php?media=wiki:latex:/imgd50830c3f8ae920ff6ceca27bcf88146.png)
Now, convert to 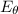 :
:
![Equations \begin{eqnarray*}
E_\theta &=& -j \omega A_T \\
A_T &=& A_z \sin \theta \\
E_\theta &=& \frac{-j \omega \mu I_0 e^{-jkr}}{2\pi r k \sin \theta} \left [ \cos \left (\frac{kL}{2} \cos \theta \right ) - \cos \left( \frac{kL}{2} \right) \right ]
\end{eqnarray*}](/wiki/lib/exe/fetch.php?media=wiki:latex:/imgc9b1c659dd16ba0d804fc6e59c1966c0.png)
This equation for 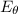 is the general form for the theta component in spherical coordinates of the far-field E field of a dipole antenna of any length oriented along the z-axis. The r component is zero due to the far-field assumption and the phi component is zero due to the electric field's orientation along the z-axis.
is the general form for the theta component in spherical coordinates of the far-field E field of a dipole antenna of any length oriented along the z-axis. The r component is zero due to the far-field assumption and the phi component is zero due to the electric field's orientation along the z-axis.